Vector3d#
- class orix.vector.Vector3d(data=None)[source]#
Bases:
Object3dThree-dimensional vectors.
Vectors \(\mathbf{v} = (x, y, z)\) support the following mathematical operations:
Unary negation.
Addition to other vectors, numbers, and compatible array-like objects.
Subtraction to and from the above.
Multiplication to numbers and compatible array-like objects.
Division by the same as multiplication. Division by a vector is not defined in general.
Examples
>>> from orix.vector import Vector3d >>> v = Vector3d([1, 2, 3]) >>> w = Vector3d([[1, 0, 0], [0, 1, 1]]) >>> w.x array([1, 0]) >>> v.unit Vector3d (1,) [[0.2673 0.5345 0.8018]] >>> -v Vector3d (1,) [[-1 -2 -3]] >>> v + w Vector3d (2,) [[2 2 3] [1 3 4]] >>> w - (2, -3) Vector3d (2,) [[-1 -2 -2] [ 3 4 4]] >>> 3 * v Vector3d (1,) [[3 6 9]] >>> v / 2 Vector3d (1,) [[0.5 1. 1.5]] >>> v / (2, -2) Vector3d (2,) [[ 0.5 1. 1.5] [-0.5 -1. -1.5]]
Vectors can be rotated by quaternion-like objects (which are interpreted as basis transformations)
>>> from orix.quaternion import Rotation >>> R = Rotation.from_axes_angles([0, 0, 1], -45, degrees=True) >>> v2 = Vector3d([1, 1, 1.]) >>> v3 = R * v2 >>> v3 Vector3d (1,) [[ 1.4142 -0. 1. ]] >>> v3_np = np.dot(R.to_matrix().squeeze(), v2.data.squeeze()) >>> np.allclose(v3.data, v3_np) True
Attributes
Azimuth spherical coordinate, i.e. the angle \(\phi \in [0, 2\pi]\) from the positive z-axis to a point on the sphere, according to the ISO 31-11 standard [Weisstein, 2005].
Return the data.
Return the number of navigation dimensions of the object.
Return the norm of the data.
Return the perpendicular vectors.
Polar spherical coordinate, i.e. the angle \(\theta \in [0, \pi]\) from the positive z-axis to a point on the sphere, according to the ISO 31-11 standard [Weisstein, 2005].
Return the radial spherical coordinate, i.e. the distance from a point on the sphere to the origin, according to the ISO 31-11 standard [Weisstein, 2005].
Return the shape of the object.
Return the total number of entries in this object.
Return the unit object.
Return or set the x coordinates.
Return the coordinates as three arrays, useful for plotting.
Return or set the y coordinates.
Return or set the z coordinate.
Methods
Vector3d.angle_with(other[, degrees])Return the angles between these vectors in other vectors.
Vector3d.cross(other)Return the cross product of a vector with another vector.
Vector3d.dot(other)Return the dot products of the vectors and the other vectors.
Vector3d.dot_outer(other[, lazy, ...])Return the outer dot products of all vectors and all the other vectors.
Vector3d.draw_circle([projection, figure, ...])Draw great or small circles with a given
opening_angleto to the vectors in the stereographic projection.Return an empty object with the appropriate dimensions.
Return a new object with the same data in a single column.
Vector3d.from_path_ends(vectors[, close, steps])Return vectors along the shortest path on the sphere between two or more consectutive vectors.
Vector3d.from_polar(azimuth, polar[, ...])Initialize from spherical coordinates according to the ISO 31-11 standard [Weisstein, 2005].
Vector3d.get_circle([opening_angle, steps])Get vectors delineating great or small circle(s) with a given
opening_angleabout each vector.Vector3d.get_nearest(x[, inclusive, tiebreak])Return the vector in
xwith the smallest angle to this vector.Vector3d.get_random_sample([size, replace, ...])Return a new flattened object from a random sample of a given size.
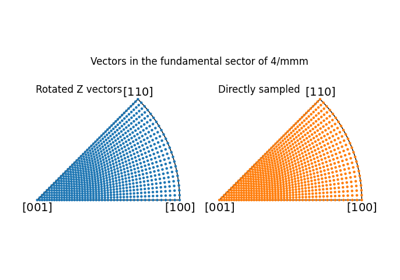
Vector3d.in_fundamental_sector(symmetry)Project vectors to a symmetry's fundamental sector (inverse pole figure).
Plot the Inverse Pole Density Function (IPDF) within the fundamental sector of a given point group symmetry in the stereographic projection.
Return the mean vector.
Vector3d.pole_density_function([resolution, ...])Plot the Pole Density Function (PDF) on a given hemisphere in the stereographic projection.
Vector3d.random([shape])Create object with random data.
Vector3d.reshape(*shape)Return a new object with the same data in a new shape.
Vector3d.rotate([axis, angle])Convenience function for rotating this vector.
Vector3d.scatter([projection, figure, ...])Plot vectors in the stereographic projection.
Return a new object with the same data with length 1-dimensions removed.
Vector3d.stack(sequence)Return a stacked object from the sequence.
Vector3d.to_polar([degrees])Return the azimuth \(\phi\), polar \(\theta\), and radial \(r\) spherical coordinates defined as in the ISO 31-11 standard [Weisstein, 2005].
Vector3d.transpose(*axes)Return a new object with the same data transposed.
Vector3d.unique([return_index, return_inverse])Return a new object containing only this object's unique entries.
Return a unit vector in the x-direction.
Return a unit vector in the y-direction.
Vector3d.zero([shape])Return zero vectors in the specified shape.
Return a unit vector in the z-direction.
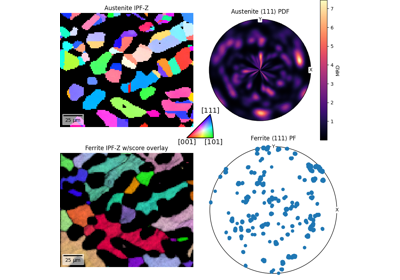
Examples using Vector3d#
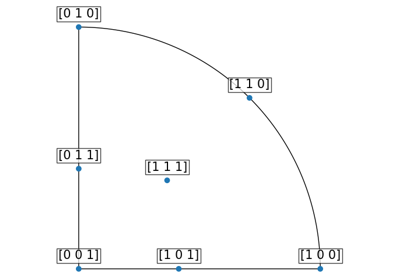
Rotating z-vector to high-symmetry crystal directions