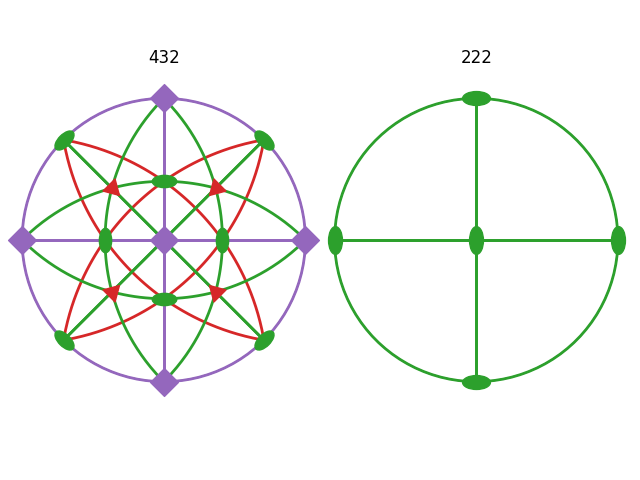
Plot symmetry operations

This example shows how to draw proper symmetry operations \(s\) (no reflections or inversions).

import matplotlib.pyplot as plt

from orix import plot
from orix.vector import Vector3d

marker_size = 200
fig, (ax0, ax1) = plt.subplots(
    ncols=2,
    subplot_kw={"projection": "stereographic"},
    layout="tight",
)

ax0.set_title("432", pad=20)
# 4-fold (outer markers will be clipped a bit...)
v4fold = Vector3d([[0, 0, 1], [1, 0, 0], [-1, 0, 0], [0, 1, 0], [0, -1, 0]])
ax0.symmetry_marker(v4fold, fold=4, c="C4", s=marker_size)
ax0.draw_circle(v4fold, color="C4")
# 3-fold
v3fold = Vector3d([[1, 1, 1], [1, -1, 1], [-1, -1, 1], [-1, 1, 1]])
ax0.symmetry_marker(v3fold, fold=3, c="C3", s=marker_size)
ax0.draw_circle(v3fold, color="C3")
# 2-fold
# fmt: off
v2fold = Vector3d(
    [
        [ 1,  0, 1],
        [ 0,  1, 1],
        [-1,  0, 1],
        [ 0, -1, 1],
        [ 1,  1, 0],
        [-1, -1, 0],
        [-1,  1, 0],
        [ 1, -1, 0],
    ]
)
# fmt: on
ax0.symmetry_marker(v2fold, fold=2, c="C2", s=marker_size)
ax0.draw_circle(v2fold, color="C2")

ax1.set_title("222", pad=20)
# 2-fold
v2fold = Vector3d([[0, 0, 1], [1, 0, 0], [-1, 0, 0], [0, 1, 0], [0, -1, 0]])
ax1.symmetry_marker(v2fold, fold=2, c="C2", s=2 * marker_size)
ax1.draw_circle(v2fold, color="C2")

Estimated memory usage: 9 MB