This page was generated from doc/tutorials/clustering_misorientations.ipynb. Interactive online version:

Clustering misorientations#

In this tutorial we will cluster Ti crystal misorientations using data obtained from a highly deformed specimen, using EBSD, as presented in [Johnstone et al., 2020]. The data can be downloaded to your local cache via the orix.data module.

Import orix classes and various dependencies

[1]:

# Exchange "inline" for "notebook" (or "qt5" from pyqt) for interactive plotting
%matplotlib inline

from matplotlib.colors import to_rgb
from matplotlib.lines import Line2D
import matplotlib.pyplot as plt
import numpy as np
from skimage.color import label2rgb
from sklearn.cluster import DBSCAN

from orix import data, plot
from orix.quaternion import Orientation, Misorientation, Rotation
from orix.quaternion.symmetry import D6
from orix.vector import Vector3d


plt.rcParams.update({"font.size": 20, "figure.figsize": (10, 10)})

Import data#

Load Ti orientations with the point group symmetry D6 (622). We have to explicitly allow downloading from an external source.

[2]:

ori = data.ti_orientations(allow_download=True)
ori

[2]:

Orientation (193167,) 622
[[ 0.3027  0.0869 -0.5083  0.8015]
 [ 0.3088  0.0868 -0.5016  0.8034]
 [ 0.3057  0.0818 -0.4995  0.8065]
 ...
 [ 0.4925 -0.1633 -0.668   0.5334]
 [ 0.4946 -0.1592 -0.6696  0.5307]
 [ 0.4946 -0.1592 -0.6696  0.5307]]

The orientations define transformations from the sample (lab) to the crystal reference frame, i.e. the Bunge convention. The above referenced paper assumes the opposite convention, which is the one used in MTEX. So, we have to invert the orientations

[3]:

ori = ~ori

Reshape the orientation mapping data to the correct spatial dimension for the scan

[4]:

ori = ori.reshape(381, 507)

Select a subset of the orientations with a suitable size for this demonstration

[5]:

ori = ori[-100:, :200]

Plot orientation maps

[6]:

ckey = plot.IPFColorKeyTSL(D6)

directions = [(1, 0, 0), (0, 1, 0)]
titles = ["X", "Y"]

fig, axes = plt.subplots(ncols=2, figsize=(15, 10))
for i, ax in enumerate(axes):
    ckey.direction = Vector3d(directions[i])
    # Invert because orix assumes lab2crystal when coloring orientations
    ax.imshow(ckey.orientation2color(~ori))
    ax.set_title(f"IPF-{titles[i]}")
    ax.axis("off")

# Add color key
ax_ipfkey = fig.add_axes(
    [0.932, 0.37, 0.1, 0.1],  # (Left, bottom, width, height)
    projection="ipf",
    symmetry=ori.symmetry.laue,
)
ax_ipfkey.plot_ipf_color_key()
ax_ipfkey.set_title("")
fig.subplots_adjust(wspace=0.01)

../_images/tutorials_clustering_misorientations_12_0.png

Map the orientations into the fundamental zone (find symmetrically equivalent orientations with the smallest angle of rotation) of D6

[7]:

ori = ori.map_into_symmetry_reduced_zone()

Compute misorientations (in the horizontal direction)

[8]:

mori_all = Misorientation(~ori[:, :-1] * ori[:, 1:])

Keep only misorientations with a disorientation angle higher than 7\(^{\circ}\), assumed to represent grain boundaries

[9]:

boundary_mask = mori_all.angle > np.deg2rad(7)
mori = mori_all[boundary_mask]

Map the misorientations into the fundamental zone of (D6, D6)

[10]:

mori.symmetry = (D6, D6)
mori = mori.map_into_symmetry_reduced_zone()

Compute distance matrix#

[11]:

# Increase the chunk size for a faster but more memory intensive computation
D = mori.get_distance_matrix()

[ ] | 0% Completed | 220.37 us: </pre>
[ ] | 0% Completed | 220.37 us: end{sphinxVerbatim}

[ ] | 0% Completed | 220.37 us

[ ] | 0% Completed | 180.98 ms: </pre>
[ ] | 0% Completed | 180.98 ms: end{sphinxVerbatim}

[ ] | 0% Completed | 180.98 ms

[ ] | 0% Completed | 348.73 ms: </pre>
[ ] | 0% Completed | 348.73 ms: end{sphinxVerbatim}

[ ] | 0% Completed | 348.73 ms

[ ] | 0% Completed | 481.25 ms: </pre>
[ ] | 0% Completed | 481.25 ms: end{sphinxVerbatim}

[ ] | 0% Completed | 481.25 ms

[ ] | 0% Completed | 618.52 ms: </pre>
[ ] | 0% Completed | 618.52 ms: end{sphinxVerbatim}

[ ] | 0% Completed | 618.52 ms

[ ] | 0% Completed | 876.44 ms: </pre>
[ ] | 0% Completed | 876.44 ms: end{sphinxVerbatim}

[ ] | 0% Completed | 876.44 ms

[ ] | 0% Completed | 993.12 ms: </pre>
[ ] | 0% Completed | 993.12 ms: end{sphinxVerbatim}

[ ] | 0% Completed | 993.12 ms

[ ] | 0% Completed | 1.10 s: </pre>
[ ] | 0% Completed | 1.10 s: end{sphinxVerbatim}

[ ] | 0% Completed | 1.10 s

[ ] | 1% Completed | 1.20 s: </pre>
[ ] | 1% Completed | 1.20 s: end{sphinxVerbatim}

[ ] | 1% Completed | 1.20 s

[ ] | 1% Completed | 1.30 s: </pre>
[ ] | 1% Completed | 1.30 s: end{sphinxVerbatim}

[ ] | 1% Completed | 1.30 s

[ ] | 2% Completed | 1.40 s: </pre>
[ ] | 2% Completed | 1.40 s: end{sphinxVerbatim}

[ ] | 2% Completed | 1.40 s

[# ] | 2% Completed | 1.50 s: </pre>
[# ] | 2% Completed | 1.50 s: end{sphinxVerbatim}

[# ] | 2% Completed | 1.50 s

[# ] | 3% Completed | 1.60 s: </pre>
[# ] | 3% Completed | 1.60 s: end{sphinxVerbatim}

[# ] | 3% Completed | 1.60 s

[# ] | 3% Completed | 1.70 s: </pre>
[# ] | 3% Completed | 1.70 s: end{sphinxVerbatim}

[# ] | 3% Completed | 1.70 s

[# ] | 4% Completed | 1.80 s: </pre>
[# ] | 4% Completed | 1.80 s: end{sphinxVerbatim}

[# ] | 4% Completed | 1.80 s

[# ] | 4% Completed | 1.91 s: </pre>
[# ] | 4% Completed | 1.91 s: end{sphinxVerbatim}

[# ] | 4% Completed | 1.91 s

[# ] | 4% Completed | 2.01 s: </pre>
[# ] | 4% Completed | 2.01 s: end{sphinxVerbatim}

[# ] | 4% Completed | 2.01 s

[## ] | 5% Completed | 2.11 s: </pre>
[## ] | 5% Completed | 2.11 s: end{sphinxVerbatim}

[## ] | 5% Completed | 2.11 s

[## ] | 5% Completed | 2.21 s: </pre>
[## ] | 5% Completed | 2.21 s: end{sphinxVerbatim}

[## ] | 5% Completed | 2.21 s

[## ] | 6% Completed | 2.31 s: </pre>
[## ] | 6% Completed | 2.31 s: end{sphinxVerbatim}

[## ] | 6% Completed | 2.31 s

[## ] | 6% Completed | 2.41 s: </pre>
[## ] | 6% Completed | 2.41 s: end{sphinxVerbatim}

[## ] | 6% Completed | 2.41 s

[## ] | 6% Completed | 2.51 s: </pre>
[## ] | 6% Completed | 2.51 s: end{sphinxVerbatim}

[## ] | 6% Completed | 2.51 s

[## ] | 7% Completed | 2.61 s: </pre>
[## ] | 7% Completed | 2.61 s: end{sphinxVerbatim}

[## ] | 7% Completed | 2.61 s

[### ] | 7% Completed | 2.72 s: </pre>
[### ] | 7% Completed | 2.72 s: end{sphinxVerbatim}

[### ] | 7% Completed | 2.72 s

[### ] | 8% Completed | 2.82 s: </pre>
[### ] | 8% Completed | 2.82 s: end{sphinxVerbatim}

[### ] | 8% Completed | 2.82 s

[### ] | 8% Completed | 2.92 s: </pre>
[### ] | 8% Completed | 2.92 s: end{sphinxVerbatim}

[### ] | 8% Completed | 2.92 s

[### ] | 8% Completed | 3.02 s: </pre>
[### ] | 8% Completed | 3.02 s: end{sphinxVerbatim}

[### ] | 8% Completed | 3.02 s

[### ] | 9% Completed | 3.12 s: </pre>
[### ] | 9% Completed | 3.12 s: end{sphinxVerbatim}

[### ] | 9% Completed | 3.12 s

[### ] | 9% Completed | 3.22 s: </pre>
[### ] | 9% Completed | 3.22 s: end{sphinxVerbatim}

[### ] | 9% Completed | 3.22 s

[#### ] | 10% Completed | 3.32 s: </pre>
[#### ] | 10% Completed | 3.32 s: end{sphinxVerbatim}

[#### ] | 10% Completed | 3.32 s

[#### ] | 10% Completed | 3.43 s: </pre>
[#### ] | 10% Completed | 3.43 s: end{sphinxVerbatim}

[#### ] | 10% Completed | 3.43 s

[#### ] | 11% Completed | 3.53 s: </pre>
[#### ] | 11% Completed | 3.53 s: end{sphinxVerbatim}

[#### ] | 11% Completed | 3.53 s

[#### ] | 11% Completed | 3.63 s: </pre>
[#### ] | 11% Completed | 3.63 s: end{sphinxVerbatim}

[#### ] | 11% Completed | 3.63 s

[#### ] | 11% Completed | 3.73 s: </pre>
[#### ] | 11% Completed | 3.73 s: end{sphinxVerbatim}

[#### ] | 11% Completed | 3.73 s

[#### ] | 12% Completed | 3.83 s: </pre>
[#### ] | 12% Completed | 3.83 s: end{sphinxVerbatim}

[#### ] | 12% Completed | 3.83 s

[##### ] | 12% Completed | 3.93 s: </pre>
[##### ] | 12% Completed | 3.93 s: end{sphinxVerbatim}

[##### ] | 12% Completed | 3.93 s

[##### ] | 13% Completed | 4.04 s: </pre>
[##### ] | 13% Completed | 4.04 s: end{sphinxVerbatim}

[##### ] | 13% Completed | 4.04 s

[##### ] | 13% Completed | 4.14 s: </pre>
[##### ] | 13% Completed | 4.14 s: end{sphinxVerbatim}

[##### ] | 13% Completed | 4.14 s

[##### ] | 13% Completed | 4.24 s: </pre>
[##### ] | 13% Completed | 4.24 s: end{sphinxVerbatim}

[##### ] | 13% Completed | 4.24 s

[##### ] | 14% Completed | 4.34 s: </pre>
[##### ] | 14% Completed | 4.34 s: end{sphinxVerbatim}

[##### ] | 14% Completed | 4.34 s

[##### ] | 14% Completed | 4.44 s: </pre>
[##### ] | 14% Completed | 4.44 s: end{sphinxVerbatim}

[##### ] | 14% Completed | 4.44 s

[##### ] | 14% Completed | 4.54 s: </pre>
[##### ] | 14% Completed | 4.54 s: end{sphinxVerbatim}

[##### ] | 14% Completed | 4.54 s

[###### ] | 15% Completed | 4.64 s: </pre>
[###### ] | 15% Completed | 4.64 s: end{sphinxVerbatim}

[###### ] | 15% Completed | 4.64 s

[###### ] | 15% Completed | 4.75 s: </pre>
[###### ] | 15% Completed | 4.75 s: end{sphinxVerbatim}

[###### ] | 15% Completed | 4.75 s

[###### ] | 16% Completed | 4.85 s: </pre>
[###### ] | 16% Completed | 4.85 s: end{sphinxVerbatim}

[###### ] | 16% Completed | 4.85 s

[###### ] | 16% Completed | 4.95 s: </pre>
[###### ] | 16% Completed | 4.95 s: end{sphinxVerbatim}

[###### ] | 16% Completed | 4.95 s

[###### ] | 17% Completed | 5.05 s: </pre>
[###### ] | 17% Completed | 5.05 s: end{sphinxVerbatim}

[###### ] | 17% Completed | 5.05 s

[####### ] | 17% Completed | 5.15 s: </pre>
[####### ] | 17% Completed | 5.15 s: end{sphinxVerbatim}

[####### ] | 17% Completed | 5.15 s

[####### ] | 17% Completed | 5.25 s: </pre>
[####### ] | 17% Completed | 5.25 s: end{sphinxVerbatim}

[####### ] | 17% Completed | 5.25 s

[####### ] | 18% Completed | 5.36 s: </pre>
[####### ] | 18% Completed | 5.36 s: end{sphinxVerbatim}

[####### ] | 18% Completed | 5.36 s

[####### ] | 18% Completed | 5.46 s: </pre>
[####### ] | 18% Completed | 5.46 s: end{sphinxVerbatim}

[####### ] | 18% Completed | 5.46 s

[####### ] | 19% Completed | 5.56 s: </pre>
[####### ] | 19% Completed | 5.56 s: end{sphinxVerbatim}

[####### ] | 19% Completed | 5.56 s

[####### ] | 19% Completed | 5.66 s: </pre>
[####### ] | 19% Completed | 5.66 s: end{sphinxVerbatim}

[####### ] | 19% Completed | 5.66 s

[######## ] | 20% Completed | 5.76 s: </pre>
[######## ] | 20% Completed | 5.76 s: end{sphinxVerbatim}

[######## ] | 20% Completed | 5.76 s

[######## ] | 20% Completed | 5.86 s: </pre>
[######## ] | 20% Completed | 5.86 s: end{sphinxVerbatim}

[######## ] | 20% Completed | 5.86 s

[######## ] | 20% Completed | 5.97 s: </pre>
[######## ] | 20% Completed | 5.97 s: end{sphinxVerbatim}

[######## ] | 20% Completed | 5.97 s

[######## ] | 21% Completed | 6.07 s: </pre>
[######## ] | 21% Completed | 6.07 s: end{sphinxVerbatim}

[######## ] | 21% Completed | 6.07 s

[######## ] | 21% Completed | 6.17 s: </pre>
[######## ] | 21% Completed | 6.17 s: end{sphinxVerbatim}

[######## ] | 21% Completed | 6.17 s

[######## ] | 22% Completed | 6.27 s: </pre>
[######## ] | 22% Completed | 6.27 s: end{sphinxVerbatim}

[######## ] | 22% Completed | 6.27 s

[######## ] | 22% Completed | 6.37 s: </pre>
[######## ] | 22% Completed | 6.37 s: end{sphinxVerbatim}

[######## ] | 22% Completed | 6.37 s

[######### ] | 22% Completed | 6.47 s: </pre>
[######### ] | 22% Completed | 6.47 s: end{sphinxVerbatim}

[######### ] | 22% Completed | 6.47 s

[######### ] | 23% Completed | 6.57 s: </pre>
[######### ] | 23% Completed | 6.57 s: end{sphinxVerbatim}

[######### ] | 23% Completed | 6.57 s

[######### ] | 23% Completed | 6.67 s: </pre>
[######### ] | 23% Completed | 6.67 s: end{sphinxVerbatim}

[######### ] | 23% Completed | 6.67 s

[######### ] | 24% Completed | 6.78 s: </pre>
[######### ] | 24% Completed | 6.78 s: end{sphinxVerbatim}

[######### ] | 24% Completed | 6.78 s

[######### ] | 24% Completed | 6.88 s: </pre>
[######### ] | 24% Completed | 6.88 s: end{sphinxVerbatim}

[######### ] | 24% Completed | 6.88 s

[########## ] | 25% Completed | 6.98 s: </pre>
[########## ] | 25% Completed | 6.98 s: end{sphinxVerbatim}

[########## ] | 25% Completed | 6.98 s

[########## ] | 25% Completed | 7.08 s: </pre>
[########## ] | 25% Completed | 7.08 s: end{sphinxVerbatim}

[########## ] | 25% Completed | 7.08 s

[########## ] | 25% Completed | 7.18 s: </pre>
[########## ] | 25% Completed | 7.18 s: end{sphinxVerbatim}

[########## ] | 25% Completed | 7.18 s

[########## ] | 26% Completed | 7.28 s: </pre>
[########## ] | 26% Completed | 7.28 s: end{sphinxVerbatim}

[########## ] | 26% Completed | 7.28 s

[########## ] | 26% Completed | 7.38 s: </pre>
[########## ] | 26% Completed | 7.38 s: end{sphinxVerbatim}

[########## ] | 26% Completed | 7.38 s

[########## ] | 27% Completed | 7.48 s: </pre>
[########## ] | 27% Completed | 7.48 s: end{sphinxVerbatim}

[########## ] | 27% Completed | 7.48 s

[########### ] | 27% Completed | 7.58 s: </pre>
[########### ] | 27% Completed | 7.58 s: end{sphinxVerbatim}

[########### ] | 27% Completed | 7.58 s

[########### ] | 27% Completed | 7.69 s: </pre>
[########### ] | 27% Completed | 7.69 s: end{sphinxVerbatim}

[########### ] | 27% Completed | 7.69 s

[########### ] | 28% Completed | 7.79 s: </pre>
[########### ] | 28% Completed | 7.79 s: end{sphinxVerbatim}

[########### ] | 28% Completed | 7.79 s

[########### ] | 28% Completed | 7.89 s: </pre>
[########### ] | 28% Completed | 7.89 s: end{sphinxVerbatim}

[########### ] | 28% Completed | 7.89 s

[########### ] | 29% Completed | 7.99 s: </pre>
[########### ] | 29% Completed | 7.99 s: end{sphinxVerbatim}

[########### ] | 29% Completed | 7.99 s

[########### ] | 29% Completed | 8.09 s: </pre>
[########### ] | 29% Completed | 8.09 s: end{sphinxVerbatim}

[########### ] | 29% Completed | 8.09 s

[############ ] | 30% Completed | 8.19 s: </pre>
[############ ] | 30% Completed | 8.19 s: end{sphinxVerbatim}

[############ ] | 30% Completed | 8.19 s

[############ ] | 30% Completed | 8.29 s: </pre>
[############ ] | 30% Completed | 8.29 s: end{sphinxVerbatim}

[############ ] | 30% Completed | 8.29 s

[############ ] | 30% Completed | 8.39 s: </pre>
[############ ] | 30% Completed | 8.39 s: end{sphinxVerbatim}

[############ ] | 30% Completed | 8.39 s

[############ ] | 31% Completed | 8.49 s: </pre>
[############ ] | 31% Completed | 8.49 s: end{sphinxVerbatim}

[############ ] | 31% Completed | 8.49 s

[############ ] | 31% Completed | 8.60 s: </pre>
[############ ] | 31% Completed | 8.60 s: end{sphinxVerbatim}

[############ ] | 31% Completed | 8.60 s

[############ ] | 32% Completed | 8.70 s: </pre>
[############ ] | 32% Completed | 8.70 s: end{sphinxVerbatim}

[############ ] | 32% Completed | 8.70 s

[############# ] | 32% Completed | 8.80 s: </pre>
[############# ] | 32% Completed | 8.80 s: end{sphinxVerbatim}

[############# ] | 32% Completed | 8.80 s

[############# ] | 32% Completed | 8.90 s: </pre>
[############# ] | 32% Completed | 8.90 s: end{sphinxVerbatim}

[############# ] | 32% Completed | 8.90 s

[############# ] | 33% Completed | 9.00 s: </pre>
[############# ] | 33% Completed | 9.00 s: end{sphinxVerbatim}

[############# ] | 33% Completed | 9.00 s

[############# ] | 33% Completed | 9.10 s: </pre>
[############# ] | 33% Completed | 9.10 s: end{sphinxVerbatim}

[############# ] | 33% Completed | 9.10 s

[############# ] | 34% Completed | 9.20 s: </pre>
[############# ] | 34% Completed | 9.20 s: end{sphinxVerbatim}

[############# ] | 34% Completed | 9.20 s

[############# ] | 34% Completed | 9.30 s: </pre>
[############# ] | 34% Completed | 9.30 s: end{sphinxVerbatim}

[############# ] | 34% Completed | 9.30 s

[############## ] | 35% Completed | 9.40 s: </pre>
[############## ] | 35% Completed | 9.40 s: end{sphinxVerbatim}

[############## ] | 35% Completed | 9.40 s

[############## ] | 35% Completed | 9.51 s: </pre>
[############## ] | 35% Completed | 9.51 s: end{sphinxVerbatim}

[############## ] | 35% Completed | 9.51 s

[############## ] | 35% Completed | 9.61 s: </pre>
[############## ] | 35% Completed | 9.61 s: end{sphinxVerbatim}

[############## ] | 35% Completed | 9.61 s

[############## ] | 36% Completed | 9.71 s: </pre>
[############## ] | 36% Completed | 9.71 s: end{sphinxVerbatim}

[############## ] | 36% Completed | 9.71 s

[############## ] | 36% Completed | 9.81 s: </pre>
[############## ] | 36% Completed | 9.81 s: end{sphinxVerbatim}

[############## ] | 36% Completed | 9.81 s

[############## ] | 37% Completed | 9.91 s: </pre>
[############## ] | 37% Completed | 9.91 s: end{sphinxVerbatim}

[############## ] | 37% Completed | 9.91 s

[############### ] | 37% Completed | 10.01 s: </pre>
[############### ] | 37% Completed | 10.01 s: end{sphinxVerbatim}

[############### ] | 37% Completed | 10.01 s

[############### ] | 37% Completed | 10.11 s: </pre>
[############### ] | 37% Completed | 10.11 s: end{sphinxVerbatim}

[############### ] | 37% Completed | 10.11 s

[############### ] | 38% Completed | 10.21 s: </pre>
[############### ] | 38% Completed | 10.21 s: end{sphinxVerbatim}

[############### ] | 38% Completed | 10.21 s

[############### ] | 38% Completed | 10.31 s: </pre>
[############### ] | 38% Completed | 10.31 s: end{sphinxVerbatim}

[############### ] | 38% Completed | 10.31 s

[############### ] | 39% Completed | 10.41 s: </pre>
[############### ] | 39% Completed | 10.41 s: end{sphinxVerbatim}

[############### ] | 39% Completed | 10.41 s

[############### ] | 39% Completed | 10.52 s: </pre>
[############### ] | 39% Completed | 10.52 s: end{sphinxVerbatim}

[############### ] | 39% Completed | 10.52 s

[################ ] | 40% Completed | 10.62 s: </pre>
[################ ] | 40% Completed | 10.62 s: end{sphinxVerbatim}

[################ ] | 40% Completed | 10.62 s

[################ ] | 40% Completed | 10.72 s: </pre>
[################ ] | 40% Completed | 10.72 s: end{sphinxVerbatim}

[################ ] | 40% Completed | 10.72 s

[################ ] | 40% Completed | 10.82 s: </pre>
[################ ] | 40% Completed | 10.82 s: end{sphinxVerbatim}

[################ ] | 40% Completed | 10.82 s

[################ ] | 41% Completed | 10.92 s: </pre>
[################ ] | 41% Completed | 10.92 s: end{sphinxVerbatim}

[################ ] | 41% Completed | 10.92 s

[################ ] | 41% Completed | 11.02 s: </pre>
[################ ] | 41% Completed | 11.02 s: end{sphinxVerbatim}

[################ ] | 41% Completed | 11.02 s

[################ ] | 42% Completed | 11.12 s: </pre>
[################ ] | 42% Completed | 11.12 s: end{sphinxVerbatim}

[################ ] | 42% Completed | 11.12 s

[################# ] | 42% Completed | 11.22 s: </pre>
[################# ] | 42% Completed | 11.22 s: end{sphinxVerbatim}

[################# ] | 42% Completed | 11.22 s

[################# ] | 43% Completed | 11.33 s: </pre>
[################# ] | 43% Completed | 11.33 s: end{sphinxVerbatim}

[################# ] | 43% Completed | 11.33 s

[################# ] | 43% Completed | 11.43 s: </pre>
[################# ] | 43% Completed | 11.43 s: end{sphinxVerbatim}

[################# ] | 43% Completed | 11.43 s

[################# ] | 43% Completed | 11.53 s: </pre>
[################# ] | 43% Completed | 11.53 s: end{sphinxVerbatim}

[################# ] | 43% Completed | 11.53 s

[################# ] | 44% Completed | 11.63 s: </pre>
[################# ] | 44% Completed | 11.63 s: end{sphinxVerbatim}

[################# ] | 44% Completed | 11.63 s

[################# ] | 44% Completed | 11.73 s: </pre>
[################# ] | 44% Completed | 11.73 s: end{sphinxVerbatim}

[################# ] | 44% Completed | 11.73 s

[################## ] | 45% Completed | 11.83 s: </pre>
[################## ] | 45% Completed | 11.83 s: end{sphinxVerbatim}

[################## ] | 45% Completed | 11.83 s

[################## ] | 45% Completed | 11.93 s: </pre>
[################## ] | 45% Completed | 11.93 s: end{sphinxVerbatim}

[################## ] | 45% Completed | 11.93 s

[################## ] | 45% Completed | 12.04 s: </pre>
[################## ] | 45% Completed | 12.04 s: end{sphinxVerbatim}

[################## ] | 45% Completed | 12.04 s

[################## ] | 46% Completed | 12.14 s: </pre>
[################## ] | 46% Completed | 12.14 s: end{sphinxVerbatim}

[################## ] | 46% Completed | 12.14 s

[################## ] | 46% Completed | 12.24 s: </pre>
[################## ] | 46% Completed | 12.24 s: end{sphinxVerbatim}

[################## ] | 46% Completed | 12.24 s

[################## ] | 47% Completed | 12.34 s: </pre>
[################## ] | 47% Completed | 12.34 s: end{sphinxVerbatim}

[################## ] | 47% Completed | 12.34 s

[################### ] | 47% Completed | 12.44 s: </pre>
[################### ] | 47% Completed | 12.44 s: end{sphinxVerbatim}

[################### ] | 47% Completed | 12.44 s

[################### ] | 47% Completed | 12.54 s: </pre>
[################### ] | 47% Completed | 12.54 s: end{sphinxVerbatim}

[################### ] | 47% Completed | 12.54 s

[################### ] | 48% Completed | 12.64 s: </pre>
[################### ] | 48% Completed | 12.64 s: end{sphinxVerbatim}

[################### ] | 48% Completed | 12.64 s

[################### ] | 48% Completed | 12.74 s: </pre>
[################### ] | 48% Completed | 12.74 s: end{sphinxVerbatim}

[################### ] | 48% Completed | 12.74 s

[################### ] | 49% Completed | 12.84 s: </pre>
[################### ] | 49% Completed | 12.84 s: end{sphinxVerbatim}

[################### ] | 49% Completed | 12.84 s

[################### ] | 49% Completed | 12.94 s: </pre>
[################### ] | 49% Completed | 12.94 s: end{sphinxVerbatim}

[################### ] | 49% Completed | 12.94 s

[#################### ] | 50% Completed | 13.05 s: </pre>
[#################### ] | 50% Completed | 13.05 s: end{sphinxVerbatim}

[#################### ] | 50% Completed | 13.05 s

[#################### ] | 50% Completed | 13.15 s: </pre>
[#################### ] | 50% Completed | 13.15 s: end{sphinxVerbatim}

[#################### ] | 50% Completed | 13.15 s

[#################### ] | 50% Completed | 13.25 s: </pre>
[#################### ] | 50% Completed | 13.25 s: end{sphinxVerbatim}

[#################### ] | 50% Completed | 13.25 s

[#################### ] | 51% Completed | 13.35 s: </pre>
[#################### ] | 51% Completed | 13.35 s: end{sphinxVerbatim}

[#################### ] | 51% Completed | 13.35 s

[#################### ] | 51% Completed | 13.45 s: </pre>
[#################### ] | 51% Completed | 13.45 s: end{sphinxVerbatim}

[#################### ] | 51% Completed | 13.45 s

[#################### ] | 52% Completed | 13.55 s: </pre>
[#################### ] | 52% Completed | 13.55 s: end{sphinxVerbatim}

[#################### ] | 52% Completed | 13.55 s

[##################### ] | 52% Completed | 13.65 s: </pre>
[##################### ] | 52% Completed | 13.65 s: end{sphinxVerbatim}

[##################### ] | 52% Completed | 13.65 s

[##################### ] | 53% Completed | 13.76 s: </pre>
[##################### ] | 53% Completed | 13.76 s: end{sphinxVerbatim}

[##################### ] | 53% Completed | 13.76 s

[##################### ] | 53% Completed | 13.86 s: </pre>
[##################### ] | 53% Completed | 13.86 s: end{sphinxVerbatim}

[##################### ] | 53% Completed | 13.86 s

[##################### ] | 53% Completed | 13.96 s: </pre>
[##################### ] | 53% Completed | 13.96 s: end{sphinxVerbatim}

[##################### ] | 53% Completed | 13.96 s

[##################### ] | 54% Completed | 14.06 s: </pre>
[##################### ] | 54% Completed | 14.06 s: end{sphinxVerbatim}

[##################### ] | 54% Completed | 14.06 s

[##################### ] | 54% Completed | 14.16 s: </pre>
[##################### ] | 54% Completed | 14.16 s: end{sphinxVerbatim}

[##################### ] | 54% Completed | 14.16 s

[###################### ] | 55% Completed | 14.26 s: </pre>
[###################### ] | 55% Completed | 14.26 s: end{sphinxVerbatim}

[###################### ] | 55% Completed | 14.26 s

[###################### ] | 55% Completed | 14.37 s: </pre>
[###################### ] | 55% Completed | 14.37 s: end{sphinxVerbatim}

[###################### ] | 55% Completed | 14.37 s

[###################### ] | 55% Completed | 14.47 s: </pre>
[###################### ] | 55% Completed | 14.47 s: end{sphinxVerbatim}

[###################### ] | 55% Completed | 14.47 s

[###################### ] | 56% Completed | 14.57 s: </pre>
[###################### ] | 56% Completed | 14.57 s: end{sphinxVerbatim}

[###################### ] | 56% Completed | 14.57 s

[###################### ] | 56% Completed | 14.67 s: </pre>
[###################### ] | 56% Completed | 14.67 s: end{sphinxVerbatim}

[###################### ] | 56% Completed | 14.67 s

[###################### ] | 57% Completed | 14.77 s: </pre>
[###################### ] | 57% Completed | 14.77 s: end{sphinxVerbatim}

[###################### ] | 57% Completed | 14.77 s

[####################### ] | 57% Completed | 14.88 s: </pre>
[####################### ] | 57% Completed | 14.88 s: end{sphinxVerbatim}

[####################### ] | 57% Completed | 14.88 s

[####################### ] | 58% Completed | 14.98 s: </pre>
[####################### ] | 58% Completed | 14.98 s: end{sphinxVerbatim}

[####################### ] | 58% Completed | 14.98 s

[####################### ] | 58% Completed | 15.08 s: </pre>
[####################### ] | 58% Completed | 15.08 s: end{sphinxVerbatim}

[####################### ] | 58% Completed | 15.08 s

[####################### ] | 58% Completed | 15.18 s: </pre>
[####################### ] | 58% Completed | 15.18 s: end{sphinxVerbatim}

[####################### ] | 58% Completed | 15.18 s

[####################### ] | 59% Completed | 15.28 s: </pre>
[####################### ] | 59% Completed | 15.28 s: end{sphinxVerbatim}

[####################### ] | 59% Completed | 15.28 s

[####################### ] | 59% Completed | 15.38 s: </pre>
[####################### ] | 59% Completed | 15.38 s: end{sphinxVerbatim}

[####################### ] | 59% Completed | 15.38 s

[######################## ] | 60% Completed | 15.48 s: </pre>
[######################## ] | 60% Completed | 15.48 s: end{sphinxVerbatim}

[######################## ] | 60% Completed | 15.48 s

[######################## ] | 60% Completed | 15.58 s: </pre>
[######################## ] | 60% Completed | 15.58 s: end{sphinxVerbatim}

[######################## ] | 60% Completed | 15.58 s

[######################## ] | 61% Completed | 15.68 s: </pre>
[######################## ] | 61% Completed | 15.68 s: end{sphinxVerbatim}

[######################## ] | 61% Completed | 15.68 s

[######################## ] | 61% Completed | 15.79 s: </pre>
[######################## ] | 61% Completed | 15.79 s: end{sphinxVerbatim}

[######################## ] | 61% Completed | 15.79 s

[######################## ] | 61% Completed | 15.89 s: </pre>
[######################## ] | 61% Completed | 15.89 s: end{sphinxVerbatim}

[######################## ] | 61% Completed | 15.89 s

[######################## ] | 62% Completed | 15.99 s: </pre>
[######################## ] | 62% Completed | 15.99 s: end{sphinxVerbatim}

[######################## ] | 62% Completed | 15.99 s

[######################### ] | 62% Completed | 16.09 s: </pre>
[######################### ] | 62% Completed | 16.09 s: end{sphinxVerbatim}

[######################### ] | 62% Completed | 16.09 s

[######################### ] | 63% Completed | 16.19 s: </pre>
[######################### ] | 63% Completed | 16.19 s: end{sphinxVerbatim}

[######################### ] | 63% Completed | 16.19 s

[######################### ] | 63% Completed | 16.29 s: </pre>
[######################### ] | 63% Completed | 16.29 s: end{sphinxVerbatim}

[######################### ] | 63% Completed | 16.29 s

[######################### ] | 63% Completed | 16.40 s: </pre>
[######################### ] | 63% Completed | 16.40 s: end{sphinxVerbatim}

[######################### ] | 63% Completed | 16.40 s

[######################### ] | 64% Completed | 16.50 s: </pre>
[######################### ] | 64% Completed | 16.50 s: end{sphinxVerbatim}

[######################### ] | 64% Completed | 16.50 s

[######################### ] | 64% Completed | 16.60 s: </pre>
[######################### ] | 64% Completed | 16.60 s: end{sphinxVerbatim}

[######################### ] | 64% Completed | 16.60 s

[########################## ] | 65% Completed | 16.70 s: </pre>
[########################## ] | 65% Completed | 16.70 s: end{sphinxVerbatim}

[########################## ] | 65% Completed | 16.70 s

[########################## ] | 65% Completed | 16.80 s: </pre>
[########################## ] | 65% Completed | 16.80 s: end{sphinxVerbatim}

[########################## ] | 65% Completed | 16.80 s

[########################## ] | 66% Completed | 16.90 s: </pre>
[########################## ] | 66% Completed | 16.90 s: end{sphinxVerbatim}

[########################## ] | 66% Completed | 16.90 s

[########################## ] | 66% Completed | 17.00 s: </pre>
[########################## ] | 66% Completed | 17.00 s: end{sphinxVerbatim}

[########################## ] | 66% Completed | 17.00 s

[########################## ] | 66% Completed | 17.10 s: </pre>
[########################## ] | 66% Completed | 17.10 s: end{sphinxVerbatim}

[########################## ] | 66% Completed | 17.10 s

[########################## ] | 67% Completed | 17.20 s: </pre>
[########################## ] | 67% Completed | 17.20 s: end{sphinxVerbatim}

[########################## ] | 67% Completed | 17.20 s

[########################### ] | 67% Completed | 17.31 s: </pre>
[########################### ] | 67% Completed | 17.31 s: end{sphinxVerbatim}

[########################### ] | 67% Completed | 17.31 s

[########################### ] | 68% Completed | 17.41 s: </pre>
[########################### ] | 68% Completed | 17.41 s: end{sphinxVerbatim}

[########################### ] | 68% Completed | 17.41 s

[########################### ] | 68% Completed | 17.51 s: </pre>
[########################### ] | 68% Completed | 17.51 s: end{sphinxVerbatim}

[########################### ] | 68% Completed | 17.51 s

[########################### ] | 69% Completed | 17.61 s: </pre>
[########################### ] | 69% Completed | 17.61 s: end{sphinxVerbatim}

[########################### ] | 69% Completed | 17.61 s

[########################### ] | 69% Completed | 17.71 s: </pre>
[########################### ] | 69% Completed | 17.71 s: end{sphinxVerbatim}

[########################### ] | 69% Completed | 17.71 s

[########################### ] | 69% Completed | 17.81 s: </pre>
[########################### ] | 69% Completed | 17.81 s: end{sphinxVerbatim}

[########################### ] | 69% Completed | 17.81 s

[############################ ] | 70% Completed | 17.92 s: </pre>
[############################ ] | 70% Completed | 17.92 s: end{sphinxVerbatim}

[############################ ] | 70% Completed | 17.92 s

[############################ ] | 70% Completed | 18.02 s: </pre>
[############################ ] | 70% Completed | 18.02 s: end{sphinxVerbatim}

[############################ ] | 70% Completed | 18.02 s

[############################ ] | 71% Completed | 18.12 s: </pre>
[############################ ] | 71% Completed | 18.12 s: end{sphinxVerbatim}

[############################ ] | 71% Completed | 18.12 s

[############################ ] | 71% Completed | 18.22 s: </pre>
[############################ ] | 71% Completed | 18.22 s: end{sphinxVerbatim}

[############################ ] | 71% Completed | 18.22 s

[############################ ] | 71% Completed | 18.32 s: </pre>
[############################ ] | 71% Completed | 18.32 s: end{sphinxVerbatim}

[############################ ] | 71% Completed | 18.32 s

[############################ ] | 72% Completed | 18.42 s: </pre>
[############################ ] | 72% Completed | 18.42 s: end{sphinxVerbatim}

[############################ ] | 72% Completed | 18.42 s

[############################# ] | 72% Completed | 18.53 s: </pre>
[############################# ] | 72% Completed | 18.53 s: end{sphinxVerbatim}

[############################# ] | 72% Completed | 18.53 s

[############################# ] | 73% Completed | 18.63 s: </pre>
[############################# ] | 73% Completed | 18.63 s: end{sphinxVerbatim}

[############################# ] | 73% Completed | 18.63 s

[############################# ] | 73% Completed | 18.73 s: </pre>
[############################# ] | 73% Completed | 18.73 s: end{sphinxVerbatim}

[############################# ] | 73% Completed | 18.73 s

[############################# ] | 74% Completed | 18.83 s: </pre>
[############################# ] | 74% Completed | 18.83 s: end{sphinxVerbatim}

[############################# ] | 74% Completed | 18.83 s

[############################# ] | 74% Completed | 18.93 s: </pre>
[############################# ] | 74% Completed | 18.93 s: end{sphinxVerbatim}

[############################# ] | 74% Completed | 18.93 s

[############################# ] | 74% Completed | 19.03 s: </pre>
[############################# ] | 74% Completed | 19.03 s: end{sphinxVerbatim}

[############################# ] | 74% Completed | 19.03 s

[############################## ] | 75% Completed | 19.13 s: </pre>
[############################## ] | 75% Completed | 19.13 s: end{sphinxVerbatim}

[############################## ] | 75% Completed | 19.13 s

[############################## ] | 75% Completed | 19.23 s: </pre>
[############################## ] | 75% Completed | 19.23 s: end{sphinxVerbatim}

[############################## ] | 75% Completed | 19.23 s

[############################## ] | 76% Completed | 19.33 s: </pre>
[############################## ] | 76% Completed | 19.33 s: end{sphinxVerbatim}

[############################## ] | 76% Completed | 19.33 s

[############################## ] | 76% Completed | 19.43 s: </pre>
[############################## ] | 76% Completed | 19.43 s: end{sphinxVerbatim}

[############################## ] | 76% Completed | 19.43 s

[############################## ] | 76% Completed | 19.54 s: </pre>
[############################## ] | 76% Completed | 19.54 s: end{sphinxVerbatim}

[############################## ] | 76% Completed | 19.54 s

[############################## ] | 77% Completed | 19.64 s: </pre>
[############################## ] | 77% Completed | 19.64 s: end{sphinxVerbatim}

[############################## ] | 77% Completed | 19.64 s

[############################### ] | 77% Completed | 19.74 s: </pre>
[############################### ] | 77% Completed | 19.74 s: end{sphinxVerbatim}

[############################### ] | 77% Completed | 19.74 s

[############################### ] | 78% Completed | 19.84 s: </pre>
[############################### ] | 78% Completed | 19.84 s: end{sphinxVerbatim}

[############################### ] | 78% Completed | 19.84 s

[############################### ] | 78% Completed | 19.94 s: </pre>
[############################### ] | 78% Completed | 19.94 s: end{sphinxVerbatim}

[############################### ] | 78% Completed | 19.94 s

[############################### ] | 79% Completed | 20.04 s: </pre>
[############################### ] | 79% Completed | 20.04 s: end{sphinxVerbatim}

[############################### ] | 79% Completed | 20.04 s

[############################### ] | 79% Completed | 20.14 s: </pre>
[############################### ] | 79% Completed | 20.14 s: end{sphinxVerbatim}

[############################### ] | 79% Completed | 20.14 s

[############################### ] | 79% Completed | 20.25 s: </pre>
[############################### ] | 79% Completed | 20.25 s: end{sphinxVerbatim}

[############################### ] | 79% Completed | 20.25 s

[################################ ] | 80% Completed | 20.35 s: </pre>
[################################ ] | 80% Completed | 20.35 s: end{sphinxVerbatim}

[################################ ] | 80% Completed | 20.35 s

[################################ ] | 80% Completed | 20.45 s: </pre>
[################################ ] | 80% Completed | 20.45 s: end{sphinxVerbatim}

[################################ ] | 80% Completed | 20.45 s

[################################ ] | 81% Completed | 20.55 s: </pre>
[################################ ] | 81% Completed | 20.55 s: end{sphinxVerbatim}

[################################ ] | 81% Completed | 20.55 s

[################################ ] | 81% Completed | 20.65 s: </pre>
[################################ ] | 81% Completed | 20.65 s: end{sphinxVerbatim}

[################################ ] | 81% Completed | 20.65 s

[################################ ] | 82% Completed | 20.75 s: </pre>
[################################ ] | 82% Completed | 20.75 s: end{sphinxVerbatim}

[################################ ] | 82% Completed | 20.75 s

[################################ ] | 82% Completed | 20.86 s: </pre>
[################################ ] | 82% Completed | 20.86 s: end{sphinxVerbatim}

[################################ ] | 82% Completed | 20.86 s

[################################# ] | 82% Completed | 20.96 s: </pre>
[################################# ] | 82% Completed | 20.96 s: end{sphinxVerbatim}

[################################# ] | 82% Completed | 20.96 s

[################################# ] | 83% Completed | 21.06 s: </pre>
[################################# ] | 83% Completed | 21.06 s: end{sphinxVerbatim}

[################################# ] | 83% Completed | 21.06 s

[################################# ] | 83% Completed | 21.16 s: </pre>
[################################# ] | 83% Completed | 21.16 s: end{sphinxVerbatim}

[################################# ] | 83% Completed | 21.16 s

[################################# ] | 84% Completed | 21.26 s: </pre>
[################################# ] | 84% Completed | 21.26 s: end{sphinxVerbatim}

[################################# ] | 84% Completed | 21.26 s

[################################# ] | 84% Completed | 21.36 s: </pre>
[################################# ] | 84% Completed | 21.36 s: end{sphinxVerbatim}

[################################# ] | 84% Completed | 21.36 s

[################################# ] | 84% Completed | 21.46 s: </pre>
[################################# ] | 84% Completed | 21.46 s: end{sphinxVerbatim}

[################################# ] | 84% Completed | 21.46 s

[################################## ] | 85% Completed | 21.56 s: </pre>
[################################## ] | 85% Completed | 21.56 s: end{sphinxVerbatim}

[################################## ] | 85% Completed | 21.56 s

[################################## ] | 85% Completed | 21.67 s: </pre>
[################################## ] | 85% Completed | 21.67 s: end{sphinxVerbatim}

[################################## ] | 85% Completed | 21.67 s

[################################## ] | 86% Completed | 21.77 s: </pre>
[################################## ] | 86% Completed | 21.77 s: end{sphinxVerbatim}

[################################## ] | 86% Completed | 21.77 s

[################################## ] | 86% Completed | 21.87 s: </pre>
[################################## ] | 86% Completed | 21.87 s: end{sphinxVerbatim}

[################################## ] | 86% Completed | 21.87 s

[################################## ] | 87% Completed | 21.97 s: </pre>
[################################## ] | 87% Completed | 21.97 s: end{sphinxVerbatim}

[################################## ] | 87% Completed | 21.97 s

[################################## ] | 87% Completed | 22.07 s: </pre>
[################################## ] | 87% Completed | 22.07 s: end{sphinxVerbatim}

[################################## ] | 87% Completed | 22.07 s

[################################### ] | 87% Completed | 22.17 s: </pre>
[################################### ] | 87% Completed | 22.17 s: end{sphinxVerbatim}

[################################### ] | 87% Completed | 22.17 s

[################################### ] | 88% Completed | 22.27 s: </pre>
[################################### ] | 88% Completed | 22.27 s: end{sphinxVerbatim}

[################################### ] | 88% Completed | 22.27 s

[################################### ] | 88% Completed | 22.37 s: </pre>
[################################### ] | 88% Completed | 22.37 s: end{sphinxVerbatim}

[################################### ] | 88% Completed | 22.37 s

[################################### ] | 89% Completed | 22.47 s: </pre>
[################################### ] | 89% Completed | 22.47 s: end{sphinxVerbatim}

[################################### ] | 89% Completed | 22.47 s

[################################### ] | 89% Completed | 22.58 s: </pre>
[################################### ] | 89% Completed | 22.58 s: end{sphinxVerbatim}

[################################### ] | 89% Completed | 22.58 s

[################################### ] | 89% Completed | 22.68 s: </pre>
[################################### ] | 89% Completed | 22.68 s: end{sphinxVerbatim}

[################################### ] | 89% Completed | 22.68 s

[#################################### ] | 90% Completed | 22.78 s: </pre>
[#################################### ] | 90% Completed | 22.78 s: end{sphinxVerbatim}

[#################################### ] | 90% Completed | 22.78 s

[#################################### ] | 90% Completed | 22.88 s: </pre>
[#################################### ] | 90% Completed | 22.88 s: end{sphinxVerbatim}

[#################################### ] | 90% Completed | 22.88 s

[#################################### ] | 91% Completed | 22.99 s: </pre>
[#################################### ] | 91% Completed | 22.99 s: end{sphinxVerbatim}

[#################################### ] | 91% Completed | 22.99 s

[#################################### ] | 91% Completed | 23.09 s: </pre>
[#################################### ] | 91% Completed | 23.09 s: end{sphinxVerbatim}

[#################################### ] | 91% Completed | 23.09 s

[#################################### ] | 92% Completed | 23.19 s: </pre>
[#################################### ] | 92% Completed | 23.19 s: end{sphinxVerbatim}

[#################################### ] | 92% Completed | 23.19 s

[#################################### ] | 92% Completed | 23.29 s: </pre>
[#################################### ] | 92% Completed | 23.29 s: end{sphinxVerbatim}

[#################################### ] | 92% Completed | 23.29 s

[##################################### ] | 92% Completed | 23.39 s: </pre>
[##################################### ] | 92% Completed | 23.39 s: end{sphinxVerbatim}

[##################################### ] | 92% Completed | 23.39 s

[##################################### ] | 93% Completed | 23.49 s: </pre>
[##################################### ] | 93% Completed | 23.49 s: end{sphinxVerbatim}

[##################################### ] | 93% Completed | 23.49 s

[##################################### ] | 93% Completed | 23.59 s: </pre>
[##################################### ] | 93% Completed | 23.59 s: end{sphinxVerbatim}

[##################################### ] | 93% Completed | 23.59 s

[##################################### ] | 94% Completed | 23.70 s: </pre>
[##################################### ] | 94% Completed | 23.70 s: end{sphinxVerbatim}

[##################################### ] | 94% Completed | 23.70 s

[##################################### ] | 94% Completed | 23.80 s: </pre>
[##################################### ] | 94% Completed | 23.80 s: end{sphinxVerbatim}

[##################################### ] | 94% Completed | 23.80 s

[##################################### ] | 94% Completed | 23.90 s: </pre>
[##################################### ] | 94% Completed | 23.90 s: end{sphinxVerbatim}

[##################################### ] | 94% Completed | 23.90 s

[###################################### ] | 95% Completed | 24.00 s: </pre>
[###################################### ] | 95% Completed | 24.00 s: end{sphinxVerbatim}

[###################################### ] | 95% Completed | 24.00 s

[###################################### ] | 95% Completed | 24.10 s: </pre>
[###################################### ] | 95% Completed | 24.10 s: end{sphinxVerbatim}

[###################################### ] | 95% Completed | 24.10 s

[###################################### ] | 96% Completed | 24.20 s: </pre>
[###################################### ] | 96% Completed | 24.20 s: end{sphinxVerbatim}

[###################################### ] | 96% Completed | 24.20 s

[###################################### ] | 96% Completed | 24.31 s: </pre>
[###################################### ] | 96% Completed | 24.31 s: end{sphinxVerbatim}

[###################################### ] | 96% Completed | 24.31 s

[###################################### ] | 97% Completed | 24.41 s: </pre>
[###################################### ] | 97% Completed | 24.41 s: end{sphinxVerbatim}

[###################################### ] | 97% Completed | 24.41 s

[###################################### ] | 97% Completed | 24.51 s: </pre>
[###################################### ] | 97% Completed | 24.51 s: end{sphinxVerbatim}

[###################################### ] | 97% Completed | 24.51 s

[####################################### ] | 97% Completed | 24.61 s: </pre>
[####################################### ] | 97% Completed | 24.61 s: end{sphinxVerbatim}

[####################################### ] | 97% Completed | 24.61 s

[####################################### ] | 98% Completed | 24.71 s: </pre>
[####################################### ] | 98% Completed | 24.71 s: end{sphinxVerbatim}

[####################################### ] | 98% Completed | 24.71 s

[####################################### ] | 98% Completed | 24.81 s: </pre>
[####################################### ] | 98% Completed | 24.81 s: end{sphinxVerbatim}

[####################################### ] | 98% Completed | 24.81 s

[####################################### ] | 99% Completed | 24.91 s: </pre>
[####################################### ] | 99% Completed | 24.91 s: end{sphinxVerbatim}

[####################################### ] | 99% Completed | 24.91 s

[####################################### ] | 99% Completed | 25.01 s: </pre>
[####################################### ] | 99% Completed | 25.01 s: end{sphinxVerbatim}

[####################################### ] | 99% Completed | 25.01 s

[####################################### ] | 99% Completed | 25.11 s: </pre>
[####################################### ] | 99% Completed | 25.11 s: end{sphinxVerbatim}

[####################################### ] | 99% Completed | 25.11 s

[########################################] | 100% Completed | 25.21 s: </pre>
[########################################] | 100% Completed | 25.21 s: end{sphinxVerbatim}

[########################################] | 100% Completed | 25.21 s

Clustering#

Apply mask to remove small misorientations associated with grain orientation spread

[12]:

small_mask = mori.angle < np.deg2rad(7)
D = D[~small_mask][:, ~small_mask]
mori = mori[~small_mask]

For parameter explanations of the DBSCAN algorithm (Density-Based Spatial Clustering for Applications with Noise), see the scikit-learn documentation.

[13]:

# Compute clusters
dbscan = DBSCAN(eps=0.05, min_samples=10, metric="precomputed").fit(D)

unique_labels, all_cluster_sizes = np.unique(
    dbscan.labels_, return_counts=True
)
print("Labels:", unique_labels)

n_clusters = unique_labels.size - 1
print("Number of clusters:", n_clusters)

Labels: [-1  0  1  2  3]
Number of clusters: 4

Calculate the mean misorientation associated with each cluster

[14]:

unique_cluster_labels = unique_labels[
    1:
]  # Without the "no-cluster" label -1
cluster_sizes = all_cluster_sizes[1:]

rc = Rotation.from_axes_angles((0, 0, 1), 15, degrees=True)

mori_mean = []
for label in unique_cluster_labels:
    # Rotate
    mori_i = rc * mori[dbscan.labels_ == label]

    # Map into the fundamental zone
    mori_i.symmetry = (D6, D6)
    mori_i = mori_i.map_into_symmetry_reduced_zone()

    # Get the cluster mean
    mori_i = mori_i.mean()

    # Rotate back and add to list
    cluster_mean_local = (~rc) * mori_i
    mori_mean.append(cluster_mean_local)

cluster_means = Misorientation.stack(mori_mean).flatten()

# Map into the fundamental zone
cluster_means.symmetry = (D6, D6)
cluster_means = cluster_means.map_into_symmetry_reduced_zone()
cluster_means

[14]:

Misorientation (4,) 622, 622
[[ 0.8467  0.2664  0.4606  0.0037]
 [-0.7858 -0.3094 -0.5355 -0.0044]
 [-0.9515 -0.3075 -0.0015 -0.007 ]
 [ 0.8656  0.4338  0.2501  0.0055]]

Inspect misorientations in the axis-angle representation

[15]:

cluster_means.axis

[15]:

Vector3d (4,)
[[0.5006 0.8656 0.007 ]
 [0.5003 0.8658 0.0072]
 [0.9997 0.0048 0.0228]
 [0.8663 0.4994 0.0109]]

[16]:

np.rad2deg(cluster_means.angle)

[16]:

array([64.29349881, 76.40971082, 35.82903611, 60.10115054])

Define reference misorientations associated with twinning orientation relationships

[17]:

# From Krakow et al.
twin_theory = Rotation.from_axes_angles(
    axes=[
        (1, 0, 0),  # sigma7a
        (1, 0, 0),  # sigma11a
        (2, 1, 0),  # sigma11b
        (1, 0, 0),  # sigma13a
        (2, 1, 0),  # sigma13b
    ],
    angles=[64.40, 34.96, 85.03, 76.89, 57.22],
    degrees=True,
)

Calculate difference, defined as minimum rotation angle, between measured and theoretical values

[18]:

mori2 = (~twin_theory).outer(cluster_means)
sym_op = D6.outer(D6).unique()
mori2_equiv = (
    D6.outer(~twin_theory).outer(sym_op).outer(cluster_means).outer(D6)
)
D2 = mori2_equiv.angle.min(axis=(0, 2, 4))

[19]:

np.rad2deg(D2)

[19]:

array([[ 0.44196598, 12.01907556, 28.59166542, 31.00602591],
       [29.33528603, 41.45127188,  1.18969475, 34.15185331],
       [37.89471722, 35.23189781, 54.83306878, 25.25351347],
       [12.60503699,  0.70196626, 41.07796156, 37.24075935],
       [27.53333357, 34.58980591, 29.35942936,  4.44471339]])

We see that the first, second, third, and fourth clusters are within \(4.5^{\circ}\) of \(\Sigma7\)a, \(\Sigma13\)a, \(\Sigma11\)a, and \(\Sigma13\)b, respectively.

Visualisation#

Associate colours with clusters for plotting

[20]:

colors = [to_rgb(f"C{i}") for i in range(cluster_means.size)]
labels_rgb = label2rgb(dbscan.labels_, colors=colors, bg_label=-1)

Inspect misorientation axes of clusters in an inverse pole figure

[21]:

cluster_sizes = all_cluster_sizes[1:]
cluster_sizes_scaled = 1000 * cluster_sizes / cluster_sizes.max()

fig, ax = plt.subplots(
    figsize=(5, 5), subplot_kw=dict(projection="ipf", symmetry=D6)
)
ax.scatter(
    cluster_means.axis, c=colors, s=cluster_sizes_scaled, alpha=0.5, ec="k"
)

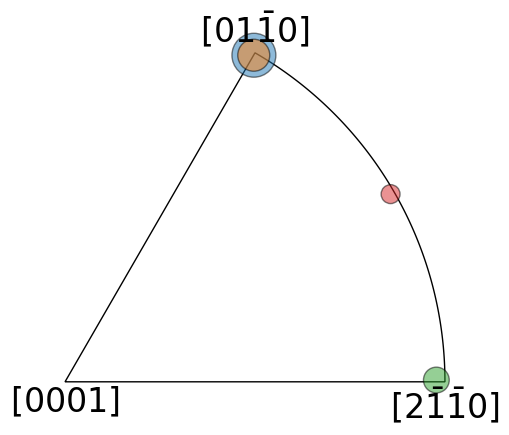
../_images/tutorials_clustering_misorientations_41_0.png

Plot a top view of the misorientation clusters within the fundamental zone for the (D6, D6) bicrystal symmetry

[22]:

wireframe_kwargs = dict(
    color="black", linewidth=0.5, alpha=0.1, rcount=361, ccount=361
)
fig = mori.scatter(
    projection="axangle",
    wireframe_kwargs=wireframe_kwargs,
    c=labels_rgb.reshape(-1, 3),
    s=4,
    alpha=0.5,
    return_figure=True,
)
ax = fig.axes[0]
ax.view_init(elev=90, azim=-60)

handle_kwds = dict(marker="o", color="none", markersize=10)
handles = []
for i in range(n_clusters):
    line = Line2D(
        [0], [0], label=i + 1, markerfacecolor=colors[i], **handle_kwds
    )
    handles.append(line)
ax.legend(
    handles=handles,
    loc="upper left",
    numpoints=1,
    labelspacing=0.15,
    columnspacing=0.15,
    handletextpad=0.05,
);

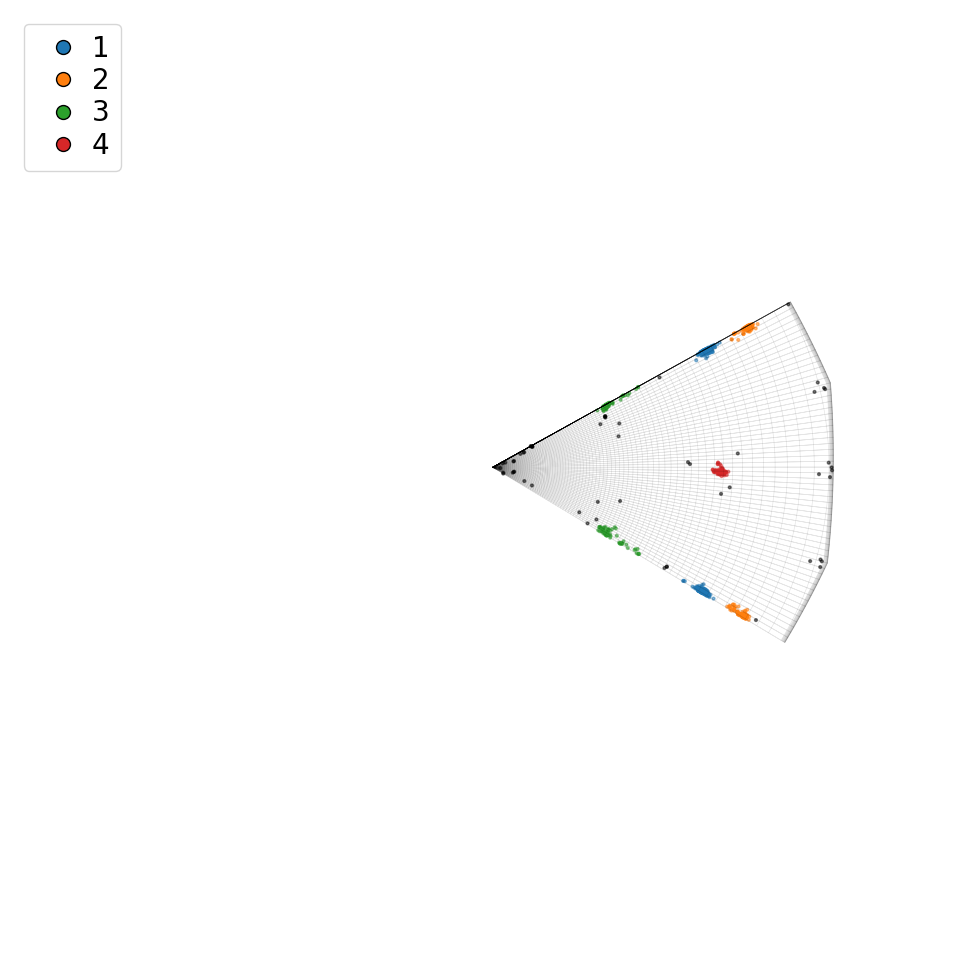
../_images/tutorials_clustering_misorientations_43_0.png

Plot side view of misorientation clusters in the fundamental zone for the (D6, D6) bicrystal symmetry

[23]:

fig2 = mori.scatter(
    return_figure=True,
    wireframe_kwargs=wireframe_kwargs,
    c=labels_rgb.reshape(-1, 3),
    s=4,
)
ax2 = fig2.axes[0]
ax2.view_init(elev=0, azim=-60)

../_images/tutorials_clustering_misorientations_45_0.png

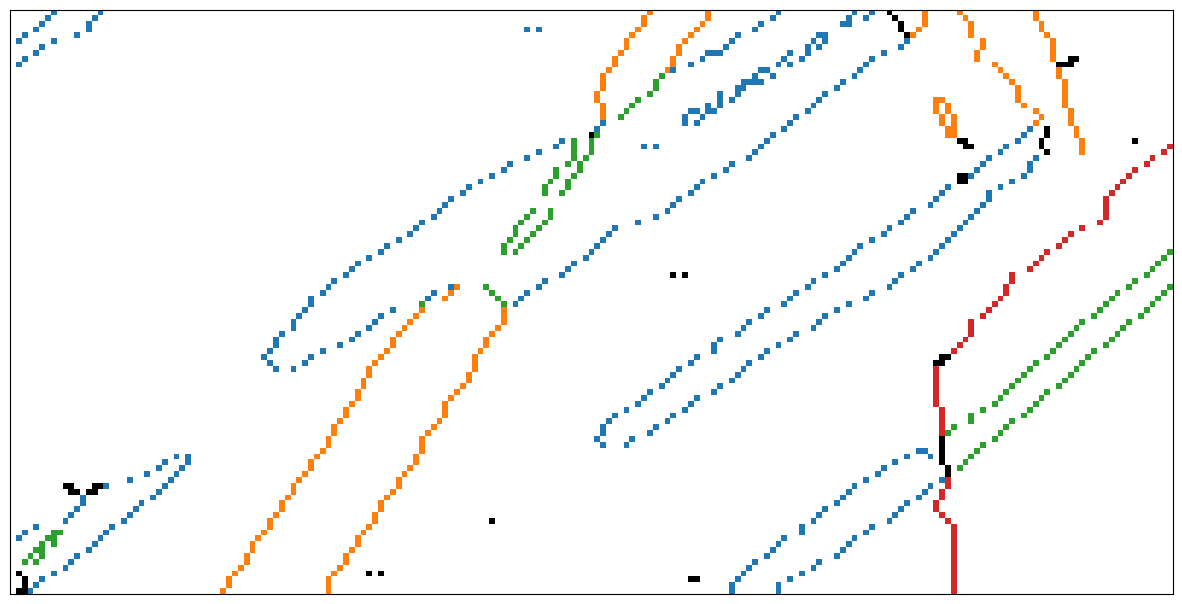
Generate map of boundaries colored according to cluster membership

[24]:

mapping = np.ones(mori_all.shape + (3,))
new_mask = (
    np.where(boundary_mask)[0][~small_mask],
    np.where(boundary_mask)[1][~small_mask],
)
mapping[new_mask] = labels_rgb

Plot map of boundaries colored according to cluster membership

[25]:

fig3, ax3 = plt.subplots(figsize=(15, 10))
ax3.imshow(mapping)
ax3.set_xticks([])
ax3.set_yticks([]);

../_images/tutorials_clustering_misorientations_49_0.png