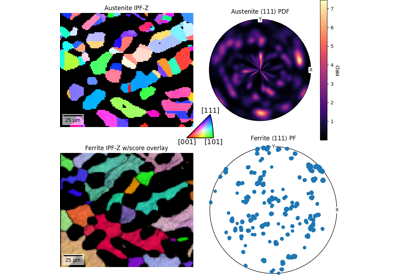
Orientation

class orix.quaternion.Orientation(data: ndarray | Misorientation | list | tuple, symmetry: Tuple[Symmetry, Symmetry] | None = None)

Bases: Misorientation

Orientations represent misorientations away from a reference of identity and have only one associated symmetry.

Orientations \(O\) support binary subtraction, producing a misorientation \(M\). That is, to compute the misorientation from \(O_1\) to \(O_2\), call O_2 - O_1.

In orix, orientations and misorientations are distinguished from rotations only by the inclusion of a notion of symmetry. Consider the following example:

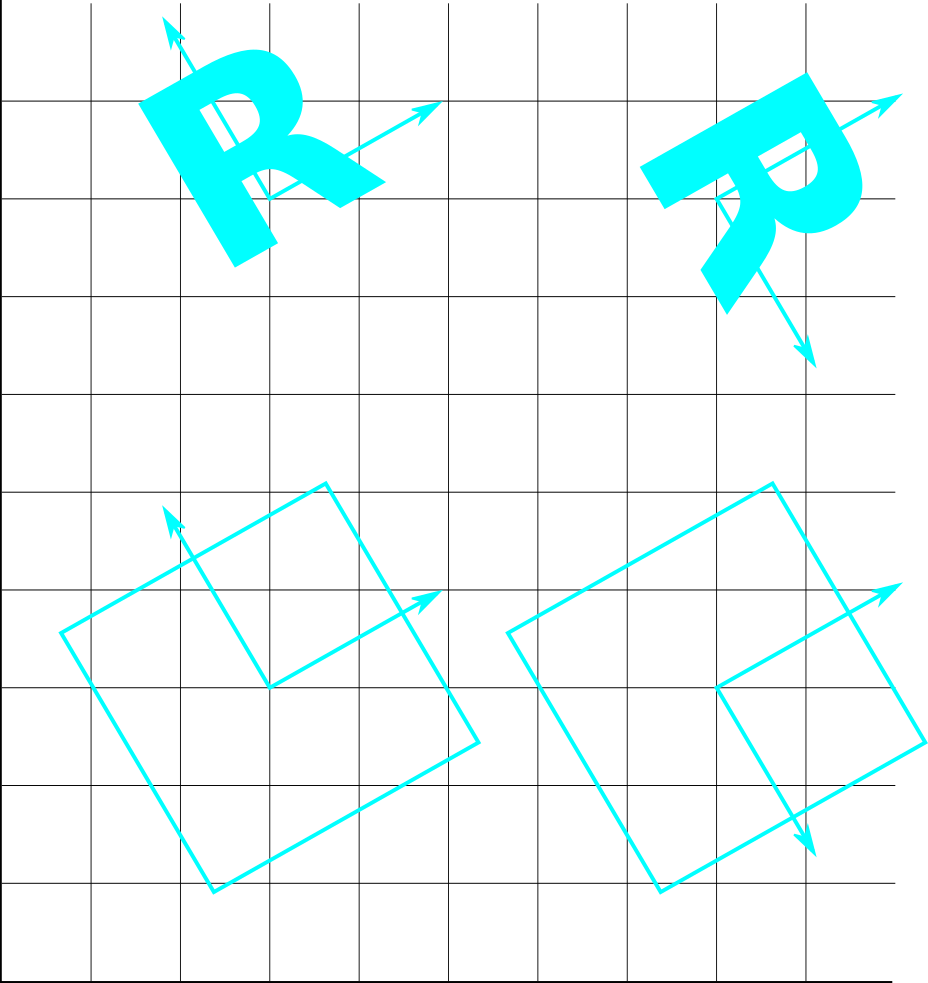
Both objects have undergone the same rotations with respect to the reference. However, because the square has four-fold symmetry, it is indistinguishable in both cases, and hence has the same orientation.

Attributes

Orientation.a	Return or set the scalar quaternion component.
Orientation.angle	Return the angle of rotation \(\omega = 2\arccos{|a|}\).
Orientation.antipodal	Return the rotation and its antipodal.
Orientation.axis	Return the axis of rotation \(\hat{\mathbf{n}} = (b, c, d)\).
Orientation.b	Return or set the first vector quaternion component.
Orientation.c	Return or set the second vector quaternion component.
Orientation.conj	Return the conjugate of the quaternion \(Q^* = a - bi - cj - dk\).
Orientation.d	Return or set the third vector quaternion component.
Orientation.data	Return the data.
Orientation.improper	Return True for improper rotations and False otherwise.
Orientation.ndim	Return the number of navigation dimensions of the object.
Orientation.norm	Return the norm of the data.
Orientation.shape	Return the shape of the object.
Orientation.size	Return the total number of entries in this object.
Orientation.symmetry	Symmetry.
Orientation.unit	Return unit orientations.

Methods

Orientation.angle_with(other[, degrees])	Return the smallest symmetry reduced angles of rotation transforming the orientations to the other orientations.
Orientation.angle_with_outer(other[, lazy, ...])	Return the symmetry reduced smallest angle of rotation transforming every orientation in this instance to every orientation in another instance.
Orientation.dot(other)	Return the symmetry reduced dot products of the orientations and the other orientations.
Orientation.dot_outer(other)	Return the symmetry reduced dot products of all orientations to all other orientations.
Orientation.empty()	Return an empty object with the appropriate dimensions.
Orientation.equivalent([grain_exchange])	Return the equivalent misorientations.
Orientation.flatten()	Return a new rotation instance collapsed into one dimension.
Orientation.from_align_vectors(other, initial)	Create an estimated orientation to optimally align vectors in the crystal and sample reference frames.
Orientation.from_axes_angles(axes, angles[, ...])	Create orientations from axis-angle pairs [Rowenhorst et al., 2015].
Orientation.from_euler(euler[, symmetry, ...])	Create orientations from sets of Euler angles [Rowenhorst et al., 2015].
Orientation.from_homochoric(ho)	Create unit quaternions from homochoric vectors \(\mathbf{h}\) [Rowenhorst et al., 2015].
Orientation.from_matrix(matrix[, symmetry])	Create orientations from orientation matrices [Rowenhorst et al., 2015].
Orientation.from_neo_euler(neo_euler[, symmetry])	[Deprecated] Create orientations from a neo-euler (vector) representation.
Orientation.from_rodrigues(ro[, angles])	Create unit quaternions from three-component Rodrigues vectors \(\hat{\mathbf{n}}\) or four-component Rodrigues-Frank vectors \(\mathbf{\rho}\) [Rowenhorst et al., 2015].
Orientation.from_scipy_rotation(rotation[, ...])	Return orientation(s) from scipy.spatial.transform.Rotation.
Orientation.get_distance_matrix([lazy, ...])	Return the symmetry reduced smallest angle of rotation transforming all these orientations to all the other orientations [Johnstone et al., 2020].
Orientation.get_random_sample([size, ...])	Return a new flattened object from a random sample of a given size.
Orientation.identity([shape])	Create identity quaternions.
Orientation.in_euler_fundamental_region()	Euler angles in the fundamental Euler region of the proper subgroup.
Orientation.inv()	Return the inverse orientations \(O^{-1}\).
Orientation.map_into_symmetry_reduced_zone([...])	Return equivalent transformations which have the smallest angle of rotation as a new misorientation.
Orientation.mean()	Return the mean quaternion with unitary weights.
Orientation.outer(other[, lazy, chunk_size, ...])	Return the outer rotation products of the rotations and the other rotations or vectors.
Orientation.plot_unit_cell([c, ...])	Plot the unit cell orientation, showing the sample and crystal reference frames.
Orientation.random([shape, symmetry])	Create random orientations.
Orientation.random_vonmises([shape, alpha, ...])	Return random rotations with a simplified Von Mises-Fisher distribution.
Orientation.reshape(*shape)	Return a new object with the same data in a new shape.
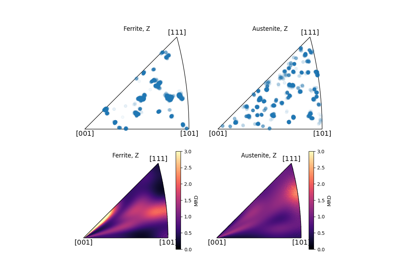
Orientation.scatter([projection, figure, ...])	Plot orientations in axis-angle space, the Rodrigues fundamental zone, or an inverse pole figure (IPF) given a sample direction.
Orientation.squeeze()	Return a new object with the same data with length 1-dimensions removed.
Orientation.stack(sequence)	Return a stacked object from the sequence.
Orientation.to_axes_angles()	Return the unit quaternions as axis-angle vectors [Rowenhorst et al., 2015].
Orientation.to_euler([degrees])	Return the unit quaternions as Euler angles in the Bunge convention [Rowenhorst et al., 2015].
Orientation.to_homochoric()	Return the unit quaternions as homochoric vectors [Rowenhorst et al., 2015].
Orientation.to_matrix()	Return the unit quaternions as orientation matrices [Rowenhorst et al., 2015].
Orientation.to_rodrigues([frank])	Return the unit quaternions as Rodrigues or Rodrigues-Frank
Orientation.transpose(*axes)	Return a new object with the same data transposed.
Orientation.triple_cross(q1, q2, q3)	Pointwise cross product of three quaternions.
Orientation.unique([return_index, ...])	Return the unique rotations from these rotations.

Examples using Orientation

Inverse pole density function

Inverse pole density function

Misorientation from aligning directions

Misorientation from aligning directions

Orientation from aligning directions

Orientation from aligning directions

Subplots

Subplots