Symmetry

class orix.quaternion.Symmetry(data: ndarray | Rotation | list | tuple)

Bases: Rotation

The set of rotations comprising a point group.

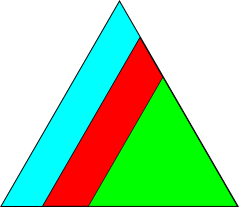
An object’s symmetry can be characterized by the transformations relating symmetrically-equivalent views on that object. Consider the following shape.

This obviously has three-fold symmetry. If we rotated it by \(\frac{2}{3}\pi\) or \(\frac{4}{3}\pi\), the image would be unchanged. These angles, as well as \(0\), or the identity, expressed as quaternions, form a group. Applying any operation in the group to any other results in another member of the group.

Symmetries can consist of rotations or inversions, expressed as improper rotations. A mirror symmetry is equivalent to a 2-fold rotation combined with inversion.

Attributes

Symmetry.a	Return or set the scalar quaternion component.
Symmetry.angle	Return the angle of rotation \(\omega = 2\arccos{|a|}\).
Symmetry.antipodal	Return the rotation and its antipodal.
Symmetry.axis	Return the axis of rotation \(\hat{\mathbf{n}} = (b, c, d)\).
Symmetry.b	Return or set the first vector quaternion component.
Symmetry.c	Return or set the second vector quaternion component.
Symmetry.conj	Return the conjugate of the quaternion \(Q^* = a - bi - cj - dk\).
Symmetry.contains_inversion	Return whether this group contains inversion.
Symmetry.d	Return or set the third vector quaternion component.
Symmetry.data	Return the data.
Symmetry.diads	Return the diads of this symmetry.
Symmetry.euler_fundamental_region	Return the fundamental Euler angle region of the proper subgroup.
Symmetry.fundamental_sector	Return the fundamental sector describing the inverse pole figure given by the point group name.
Symmetry.improper	Return True for improper rotations and False otherwise.
Symmetry.is_proper	Return whether this group contains only proper rotations.
Symmetry.laue	Return this group plus inversion.
Symmetry.laue_proper_subgroup	Return the proper subgroup of this group plus inversion.
Symmetry.ndim	Return the number of navigation dimensions of the object.
Symmetry.norm	Return the norm of the data.
Symmetry.order	Return the number of elements of the group.
Symmetry.proper_subgroup	Return the largest proper group of this subgroup.
Symmetry.proper_subgroups	Return the list of proper groups that are subgroups of this group.
Symmetry.shape	Return the shape of the object.
Symmetry.size	Return the total number of entries in this object.
Symmetry.subgroups	Return the list groups that are subgroups of this group.
Symmetry.system	Return which of the seven crystal systems this symmetry belongs to.
Symmetry.unit	Return the unit object.

Methods

Symmetry.angle_with(other[, degrees])	Return the angles of rotation transforming the rotations to the other rotations.
Symmetry.angle_with_outer(other[, degrees])	Return the angles of rotation transforming the rotations to all the other rotations.
Symmetry.dot(other)	Return the dot products of the quaternions and the other quaternions.
Symmetry.dot_outer(other)	Return the outer dot products of the rotations and the other rotations.
Symmetry.empty()	Return an empty object with the appropriate dimensions.
Symmetry.flatten()	Return a new rotation instance collapsed into one dimension.
Symmetry.from_align_vectors(other, initial)	Estimate a quaternion to optimally align two sets of vectors.
Symmetry.from_axes_angles(axes, angles[, ...])	Create unit quaternions from axis-angle pairs \((\hat{\mathbf{n}}, \omega)\) [Rowenhorst et al., 2015].
Symmetry.from_euler(euler[, direction, degrees])	Create unit quaternions from Euler angle sets [Rowenhorst et al., 2015].
Symmetry.from_generators(*generators)	Create a Symmetry from a minimum list of generating transformations.
Symmetry.from_homochoric(ho)	Create unit quaternions from homochoric vectors \(\mathbf{h}\) [Rowenhorst et al., 2015].
Symmetry.from_matrix(matrix)	Create unit quaternions from orientation matrices [Rowenhorst et al., 2015].
Symmetry.from_neo_euler(neo_euler)	[Deprecated] Create unit quaternion(s) from a neo-euler (vector) representation.
Symmetry.from_rodrigues(ro[, angles])	Create unit quaternions from three-component Rodrigues vectors \(\hat{\mathbf{n}}\) or four-component Rodrigues-Frank vectors \(\mathbf{\rho}\) [Rowenhorst et al., 2015].
Symmetry.from_scipy_rotation(rotation)	Create unit quaternions from scipy.spatial.transform.Rotation.
Symmetry.fundamental_zone()
Symmetry.get_axis_orders()
Symmetry.get_highest_order_axis()
Symmetry.get_random_sample([size, replace, ...])	Return a new flattened object from a random sample of a given size.
Symmetry.identity([shape])	Create identity quaternions.
Symmetry.inv()	Return the inverse rotations \(R^{-1}\).
Symmetry.mean()	Return the mean quaternion with unitary weights.
Symmetry.outer(other[, lazy, chunk_size, ...])	Return the outer rotation products of the rotations and the other rotations or vectors.
Symmetry.plot([orientation, ...])	Stereographic projection of symmetry operations.
Symmetry.random([shape])	Create object with random data.
Symmetry.random_vonmises([shape, alpha, ...])	Return random rotations with a simplified Von Mises-Fisher distribution.
Symmetry.reshape(*shape)	Return a new object with the same data in a new shape.
Symmetry.squeeze()	Return a new object with the same data with length 1-dimensions removed.
Symmetry.stack(sequence)	Return a stacked object from the sequence.
Symmetry.to_axes_angles()	Return the unit quaternions as axis-angle vectors [Rowenhorst et al., 2015].
Symmetry.to_euler([degrees])	Return the unit quaternions as Euler angles in the Bunge convention [Rowenhorst et al., 2015].
Symmetry.to_homochoric()	Return the unit quaternions as homochoric vectors [Rowenhorst et al., 2015].
Symmetry.to_matrix()	Return the unit quaternions as orientation matrices [Rowenhorst et al., 2015].
Symmetry.to_rodrigues([frank])	Return the unit quaternions as Rodrigues or Rodrigues-Frank
Symmetry.transpose(*axes)	Return a new object with the same data transposed.
Symmetry.triple_cross(q1, q2, q3)	Pointwise cross product of three quaternions.
Symmetry.unique([return_index, ...])	Return the unique rotations from these rotations.

Examples using Symmetry

Inverse pole density function

Inverse pole density function

Subplots

Subplots

Rotations mapping the fundamental sector on S2

Rotations mapping the fundamental sector on S2

Restrict to fundamental sector

Restrict to fundamental sector